Differenzialrechnung
Monopolmodell
Preisabsatzfunktion
Gegeben |
|||||||||||||||||||||
|
Gegeben ist, dass man bei einem Absatz von 2 ME einen Erlös von 30 GE und bei 4 ME einen Erlös von 24 GE macht. |
||||||||||||||||||||
Das bedeutet |
|||||||||||||||||||||
|
Mit den gegebenen Angaben bilden wir Punkte, wobei die ME den x-Wert und die GE den y-Wert darstellen. |
||||||||||||||||||||
Einsetzen der Punkte in die Zwei-Punkte-Formel |
|||||||||||||||||||||
|
Um nun die Preisabsatzfunktion zu ermitteln setzen wir die beiden Punkte in die Zwei-Punkte-Formel ein. Da wir es mit einem Monopolmodell zu tun haben ist die Preisabsatzfunktion linear. |
Kostenfunktion
Gegeben |
|||||||||||||||||||||
|
Gegeben ist, dass man bei einem Absatz von 0 ME Kosten in Höhe von 30 GE und bei 4 ME Kosten in Höhe von 62 GE hat. |
||||||||||||||||||||
Das bedeutet |
|||||||||||||||||||||
|
Mit den gegebenen Angaben bilden wir Punkte, wobei die ME den x-Wert und die GE den y-Wert darstellen. |
||||||||||||||||||||
Einsetzen der Punkte in die Zwei-Punkte-Formel |
|||||||||||||||||||||
|
Um nun die Kostenfunktion zu ermitteln setzen wir die beiden Punkte in die Zwei-Punkte-Formel ein. |
Gesamterlösfunktion
|
Um die Gesamterlösfunktion zu ermitteln gehen wir immer nach dem gleichen Schema vor: Gesamterlösfunktion = x · Preisabsatzfunktion |
|||||||||||||||
Erlösmaximum |
||||||||||||||||
|
Das Erlösmaximum gibt an, an welchem Punkt ein Unternehmen den höchsten Erlös erzielt. Nach diesem Punkt sinkt die Erlöskurve wieder. Es wird berechnet, indem man das Extremum der Erlösfunktion berechnet. Dies tut man, indem man die x-Werte der ersten Ableitung der Erlösfunktion errechnet und diesen dann in die Erlösfunktion einsetzt, um den y-Wert zu erhalten, der zur Bildung eines Punktes notwendig ist. |
|||||||||||||||
Gewinnfunktion
|
Um die Gewinnfunktion zu ermitteln benutzen wir immer das gleiche Schema: Gewinnfunktion = Erlösfunktion - Kostenfunktion |
||||||||||||||||||||
Nutzschwelle und Nutzgrenze |
|||||||||||||||||||||
|
Die Nutzschwelle und die Nutzgrenze sind die Nullstellen der Gewinnfunktion. Die Nutzschwelle gibt an, ab wann ein Unternehmen mit seiner Produktion in den Gewinnbereich eintritt. Die Nutzgrenze gibt an, ab wann ein Unternehmen mit seiner Produktion den Gewinnbereich verlässt. |
||||||||||||||||||||
Gewinnmaximum |
|||||||||||||||||||||
|
Das Gewinnmaximum gibt an, an welchem Punkt ein Unternehmen den höchsten Gewinn erzielt. Nach diesem Punkt sinkt die Gewinnkurve wieder. Es wird berechnet, indem man das Extremum der Gewinnfunktion berechnet. Dies tut man, indem man die x-Werte der ersten Ableitung der Gewinnfunktion errechnet und diesen dann in die Gewinnfunktion einsetzt, um den y-Wert zu erhalten, der zur Bildung eines Punktes notwendig ist. |
||||||||||||||||||||
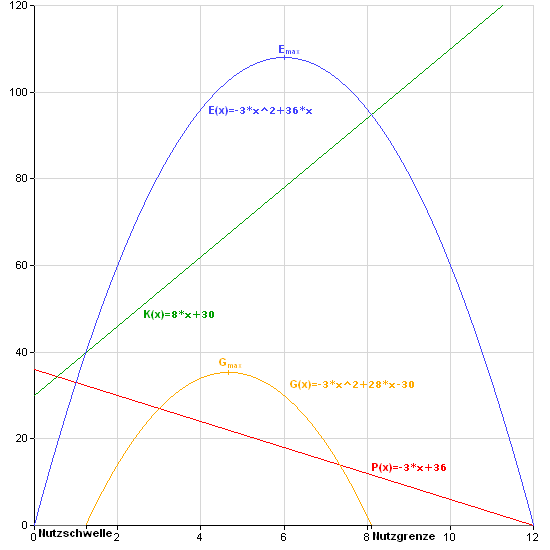
Graphische Darstellung