Orthogonalität
Die Projektion
Sprechen wir über die Projektion, die ein Vektor auf einen anderen wirft so reden wir automatisch vom Skalarprodukt. Um ein Einblick in dieses Thema zu bekommen schauen wir uns erst einmal folgendes Bild an:
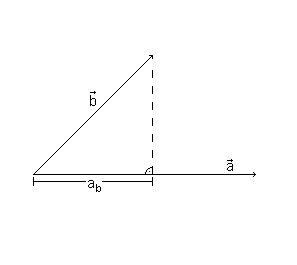
Auf dem Bild sehen wir den Vektor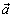
und den Vektor
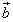, die nicht senkrecht zueinander sind. Desweiteren sehen wir die Strecke
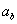. Diese Strecke stellt die Projektion des Vektors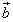auf den Vektor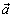dar.
Was das ganze mit dem Skalarprodukt zu tun hat soll diese Formel veranschaulichen:
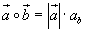
Im Klartext bedeutet das, dass das Skalarprodukt der Betrag des Vektors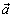mal die Strecke 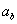ist. (Für diese Aussage gibt es hier keine Erklärung also nicht verzweifelt versuchen diese Formel aus dem Bild abzuleiten sondern einfach akzeptieren)
Wer jetzt mitdenkt erkennt, dass wir wenn die Vektoren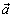und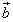gegeben sind ganz leicht die Strecke 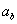, sprich die Länge der Projektion von 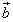auf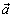herausfinden können indem wir 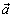und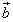miteinander skalarmultiplizieren und dann durch den Betrag von 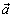teilen. Hört sich schwierig an? Hier noch einmal in Rechenform und mit gegebenen Vektoren:
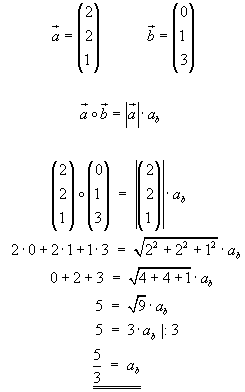
Übertragung auf die Ebene
|
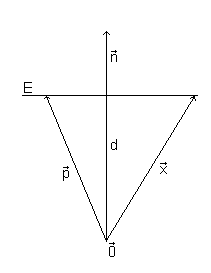
Wir gehen nun davon aus, dass sowohl Wenn also beide Vektoren auf der Ebene liegen ist ihre Skalarmultiplikation mit Das folgende Bild zeigt das linke Bild in der zweiten Dimension. Vielleicht hilft es dem Verständnis:
|
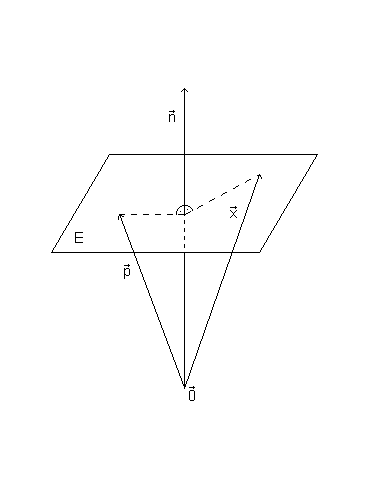
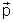als auch
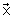auf der Ebene liegen.
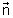gleich groß und die Projektion (in diesem Fall sprechen wir von d) der Vektoren auf
