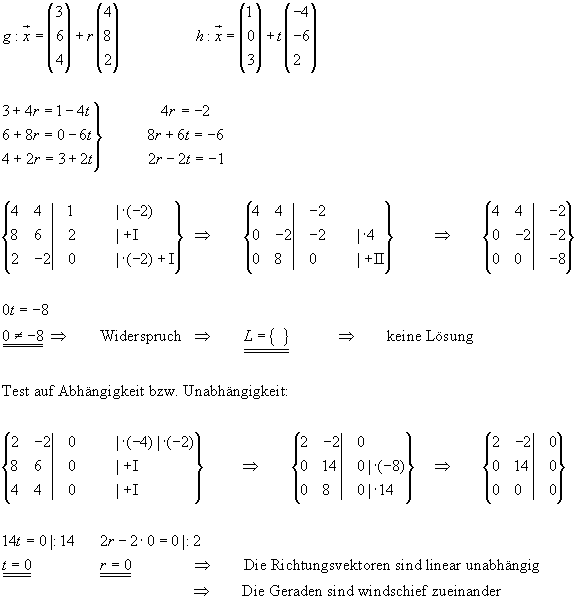Lineare Algebra
Gegenseitige Lage von Geraden
Zwei im Raum liegende Geraden fallen entweder zusammen, schneiden sich oder sind parallel zu einander. Bei zwei Geraden des Raumes kann auch der Fall eintreten, dass sie weder zueinander parallel sind, noch gemeinsame Schnittpunkte besitzen. Solche Geraden heißen zueinander windschief. Es gibt also vier mögliche verschiedene Geraden im Raum.
Schnittpunkt
Für die Geraden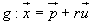 
und 
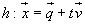gilt:
G und h schneiden sich in einem Punkt, wenn die Vektorgleichung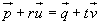 
genau eine Lösung für r und t hat.
Beispiel:
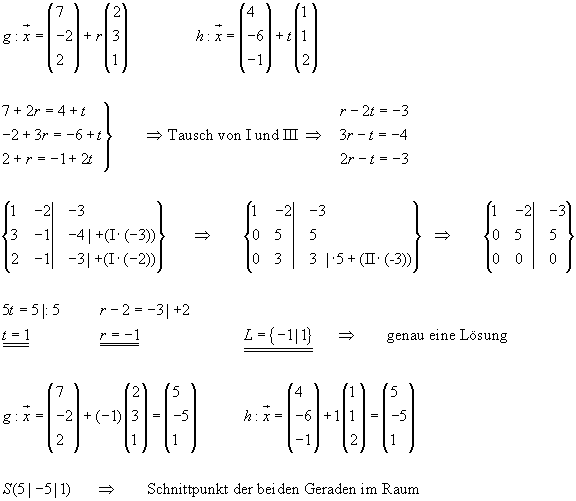
Identisch
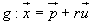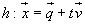Für die Geraden und gilt:
G und h sind identisch (d.h. sie liegen ineinander), wenn die Vektorgleichung 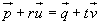unendlich viele Lösungen hat.
Beispiel:
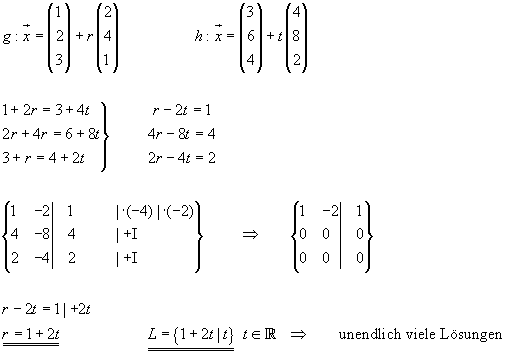
Parallel
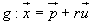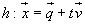Für die Geraden und gilt:
G und h haben keinen gemeinsamen Punkt und sind parallel zueinander, wenn die Vektorgleichung 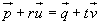keine Lösung hat.
Wenn Parallelität vorliegt, müssen die Richtungsvektoren der beiden Geraden linear abhängig voneinander sein.
Beispiel:
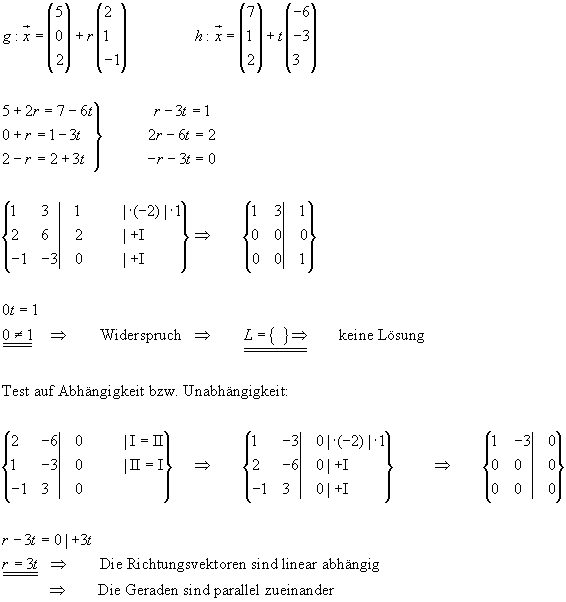
Windschief
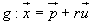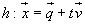Für die Geraden und gilt:
G und h haben keinen gemeinsamen Punkt, d.h sie sind zueinander windschief, wenn die Vektorgleichung 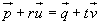keine Lösung hat.
Wenn die Geraden zueinander windschief liegen, müssen die Richtungsvektoren der beiden Geraden linear unabhängig voneinander sein.
Beispiel:
